​美妙数学之柳卡图，一张图解决一类问题，凸显数形结合的超级魅力

美妙数学之柳卡图，一张图解决一类问题，凸显数形结合的超级魅力

这是一个刷题的时代，老师刷题，以为从此天下无题不解。学生刷题，以为是提高解题能力的速成宝典。于是刷题风起，把刷题当作学习数学的魔方，把题海捧为成就学霸的金丹。大海茫茫靠灯塔，题海茫茫凭典例，殊不知一道题做'透'了，要远胜过做一百道题。刷百题不如解透一题，多做题固然必不可少，但多反思更难能可贵。

行程问题在中小学阶段是一个比较典型的知识点，很多同学在学习的时候都遇到了不小的挑战。究其原因，一是主要因为学过知识没有得到有效运用以及缺少充分的实操机会，二是因为掌握解题技巧有限。今天分享一类有趣的问题，一个巧妙的方法，一起感受数形结合的力量。

在十九世纪的一次国际科学会议期间，一天，当来自世界各国的许多著名数学家的晨宴快要结束的时候，法国数学家柳卡突然向在场的人们提出了一个被他称为"最困难"的问题：假定某轮船公司较长时间以来，每天中午都有一艘轮船从哈佛开往纽约，并且在每天的同一时刻也有一艘轮船从纽约开往哈佛。轮船在途中所花的时间，来去都是七昼夜，而且都是匀速航行在同一条航线上。问今天中午从哈佛开出的轮船，在开往纽约的整个运途中，将会遇到几艘同一公司的轮船从对面开来？

这个问题之所以有趣，是因为看似容易，实则易错。

在那次国际会议上，有几位学者回答，会遇上7艘轮船。这个答案是错误的，其原因是，仅考虑了它开出后的七天里从纽约驶往哈佛的轮船，而忽略了已在海上航行着的轮船。

经过一番思考后，又有人提出了"遇到14艘轮船"的回答。这个回答是前进了一大步，但仍是错误的。为得出正确的解答，我们采用图解法。

在tos平面上，ot轴代表时间，os轴代表路程。o点代表轮船在哈佛出发的那一天，右边的正数代表出发后的天数，左边的负数的绝对值则代表出发前的第几天。另在os轴上任选一点作为纽约的位置。从左上方画向右下方的那簇平行线就是我们说的那艘轮船出发前后若干天内从纽约开往哈佛的各艘轮船的路程曲线。从o点向右上方画出的那条带箭头的斜线，就是从哈佛到纽约的那艘轮船的路程曲线。

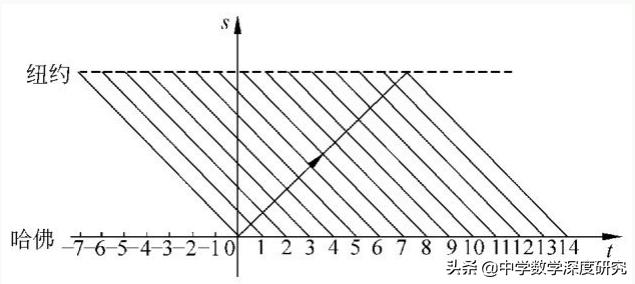
观图可知，这艘轮船将遇到15艘从纽约开往哈佛的轮船。第1艘是在出发时遇到的，第15艘是在到达纽约时遇到的，中间的13艘是在海上遇到的。而且相遇的时间是在每天的中午和子夜。

简化图形解法如下：

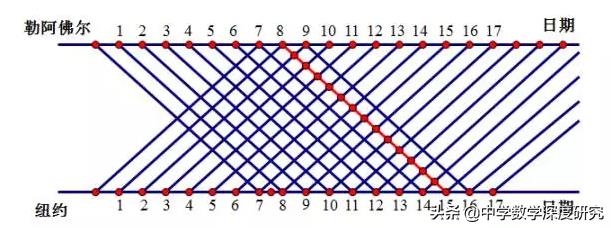
柳卡问题有很多解法，其中图示法是一种比较通用的解法，该图称为柳卡图，也称为折线图，可以很好的解决复杂的行程问题。

快速的解法是直接画时间一距离图，再画上密密麻麻的交叉线，按要求数交点个数即可完成。折线示意图往往能够清晰的体现运动过程中"相遇的次数"，"相遇的地点"，以及"由相遇的地点求出全程"，使用折线示意图法一般需要我们知道每个物体走完一个全程时所用的时间是多少。其中涉及到距离的问题还可以借助几何中沙漏原理来获取。

例.一条电车线路的起点站和终点站分别是甲站和乙站，每隔5分钟有一辆电车从甲站发出开往乙站，全程要走15分钟。有一个人从乙站出发沿电车线路骑车前往甲站．他出发的时候，恰好有一辆电车到达乙站．在路上他又遇到了10辆迎面开来的电车．到达甲站时，恰好又有一辆电车从甲站开出．问他从乙站到甲站用了多少分钟？

解析：一条电车线路的起点站和终点站分别是甲站和乙站，每隔5分钟有一辆电车从甲站发出开往乙站，全程要走15分钟，所以骑车人一共看到12辆车，他出发时看到的是15分钟前发的车，此时第4辆车正从甲发出。骑车中，甲站发出第4到第12辆车，共9辆，有8个5分钟的间隔，时间是（40分钟）。

用柳卡图解答如下：

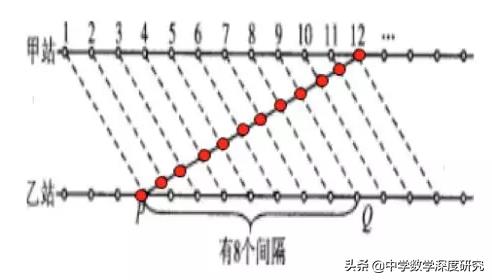
变式1. 一辆公共汽车12：00开始从A车站出发，往返于AB两个公交车站之间，若从A到B用3个小时，从B到A用4个小时。有一个行人13：00时从B车站步行去A车站，已知他花了8个小时到达A车站。问：途中，他遇到几次这辆公共汽车？

解析：可以做出如下六卡图：

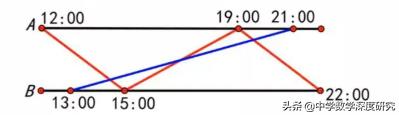
题目并未说明公共汽车和行人是匀速前进，所以图中的线段不一定是直的

但是无论是否是直线段，因为在这几个特定时间点车和人都到达特定车站，所以途中一定会遇到如图的3次。

变式2. A、B两地每隔五分钟有一辆车发出，匀速对开且所有班车的速度都相同，甲乙两人同时从A、B两地出发，相向匀速而行。甲、乙出发后五分钟，两地同时开出第一辆班车；甲、乙相遇时，甲被A地开出的第9辆车追上，乙也恰好被B地开出的第6辆车追上。乙到A地时，恰好被B地开出的第8辆车追上，而此时甲距B地还有21千米，乙速度为______千米/时。

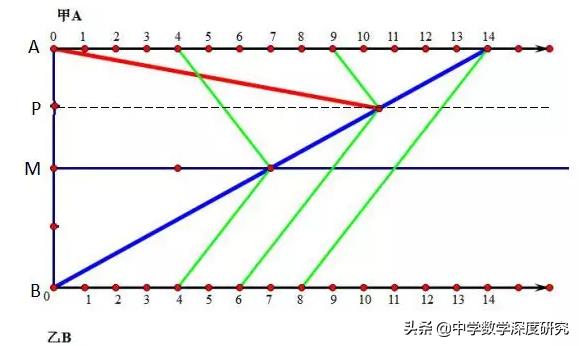
变式3. 小山小林在宿舍和食堂往返跑。小林从宿舍出发，小山从食堂出发，小山的速度是小林的3倍，第100次相遇时，离宿舍60米，问全程多长？

解析：两条相互平行的横线之间的距离代表全程长度，线上向右的等距离的小格代表时间的流程，画出1个循环的柳卡图，如下：

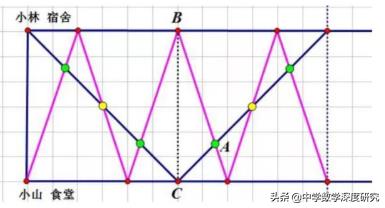
一个循环内，4次迎面相遇、2次后面追上，共计6次相遇。100÷6=16…4，第100次相遇在A点，小山从B到A的距离是60米。小山从B到A，相同的时间内，小林从C到A，因为小山的速度是小林的3倍，所以C到A的距离为60÷3=20米。全程：60+20=80（米）。

柳卡图是解决多次相遇问题时经常运用的一种方法，它利用数形结合的思想，让我们能轻松地看出相遇的次数。在画柳卡图时有以下几个步骤：

1. 先计算两个运动物体行完一个全程的时间；

2. 先画出其中一个运动物体来回运动的路线，再用另一种线形或颜色画出另一个物体的运动路线；

3. 图中两个物体运动路线交叉的地方就是他们相遇的点，如果时间较长可以先画出第一个周期，再进行计算。

注意事项

（1）明确时间及时间关系是柳卡图的前提。

要想画出柳卡图，必须先计算出两个运动对象行完一个全程的时间。这里的时间既可以是具体的时间（例如：甲从A到B需要8分钟，乙从B到A需要5分钟），也可以是一种时间关系（例如：甲乙两人的速度比是4：3，则甲从A到B需要3份时间，乙从B到A需要4份时间）。

（2）区分两个运动对象和明确相遇次数。

画图时，可采用不同颜色或线型来区分两个运动对象，然后在交点处标注数字来表示相遇的次数。

（3）区分匀速往返和变逸往返。

匀速往返是指在往返的过程中始终保持原来的速度行驶，匀速往返所色出的线段是等长的；变速往返是指在往返的过程中出现加速或降速行驶的情况，变速往返所画出的线段是不等长的。

（4）明确相遇点距离起点或终点的距离。

相遇点到起（终）点的距离就是过相遇点作起（终）点所在时间轴（射线）的垂线，其中垂线段的长度表示相遇点到起（终）点的距离。

（5）明确一个往返周期的时间节点。

如果计算的时间段较长，可以只画出一个往返周期。然后通过对一个往返周期规律的研究，计算整个时间段的相遇次数。通常，一个往返周期是指两个运动对象同时从出发点出发，到各自同时回到出发点为止。

因为用交点表示相遇，所以柳卡图很适合解决多次相遇问题，尤其是解决相遇次数时尤为有效，凸显数形结合思想解题魅力。

可以说"数"与"形"反映了事物两个方面的属性。我们认为，数形结合，主要指的是数与形之间的一一对应关系。数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来，通过"以形助数"或"以数解形"即通过抽象思维与形象思维的结合，可以使复杂问题简单化，抽象问题具体化，从而实现优化解题途径的目的。